
희소 행렬 (Sparse Matrix)이란?
희소 행렬이란 행렬의 값이 대부분 0인 경우를 가리키는 표현으로 '성긴 행렬'이라고도 불린다. 전체 행렬의 값 중에 0인 요소들의 비율을 희소성 (sparsity)라고 하며 행렬에 0이 많이 포함될 수록 희소성이 높다고 할 수 있다.
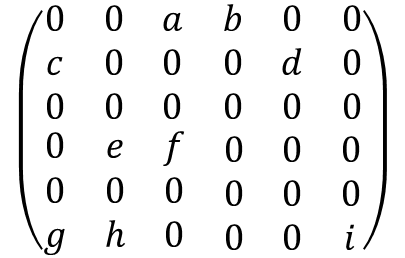
희소 행렬은 그 자체로 수학적인 관점에서 큰 의미를 가지고 있지 않을 수 있지만 인접 행렬 (Adjacency matrix)과 같이 현실에 존재하는 특정한 관계성을 표현하는 과정에서는 흔히 등장하는 개념이다. 예를 들어, e-commerce 서비스에서 각 유저가 구입한 상품의 수를 행렬로 표현한다면 각 유저는 모든 상품 중 일부만 구입할 것이므로 그 행렬은 희소 행렬에 가까울 것이다. 마찬가지로 넷플릭스나 tving과 같은 OTT 서비스에서 유저와 시청 기록의 관계를 행렬로 표현하더라도 그 행렬의 희소성은 매우 높을 것이다. 이외에도 문서를 단어의 빈도수로 표현하는 document-term matrix나 Relu 기반의 activation function을 사용하는 neural networks의 activation map에서도 희소 행렬은 쉽게 찾아볼 수 있다.
문제는 희소 행렬은 너무 많은 요소를 0으로 가지고 있기 때문에 컴퓨터에서 이를 표현하고자 할 때 실제로 포함하고 있는 정보의 양에 비해 메모리를 과하게 사용한다는 점이다. 따라서 희소 행렬을 다루는 프로그램을 작성할 때에는 메모리를 효율적으로 관리하기 위해 몇 가지 방식이 적용된다.
COO vs CSR vs DCSR Matrix
희소 행렬을 메모리 효율적으로 표현하는 방식에는 몇 가지 포맷이 있는데, 그중 대표적으로 3가지 방식을 본 글에서 설명하고자 한다.
- Coordinate format (COO Matrix)
- Compressed Sparse Row format (CSR Matrix)
- Dynamic Sparse Row format (DCSR Matrix)
이외에도 희소 행렬을 위한 다양한 표현 형태가 존재하고 python의 scipy 라이브러리에서도 다양한 희소 행렬을 위한 클래스를 제공한다. 각 형태는 sparsity나 데이터 사이즈에 따라 장단점이 존재하고 메모리를 적게 사용하는 형태가 있는가 하면 메모리는 좀 더 사용하지만 특정 연산에 우수한 형태도 존재한다.
우선 위의 세 가지 형태 (COO, CSR, DCSR)에 대한 설명을 위해 위에서 예시로 등장한 희소 행렬을 조금 더 시각적으로 표현하면 다음과 같다.
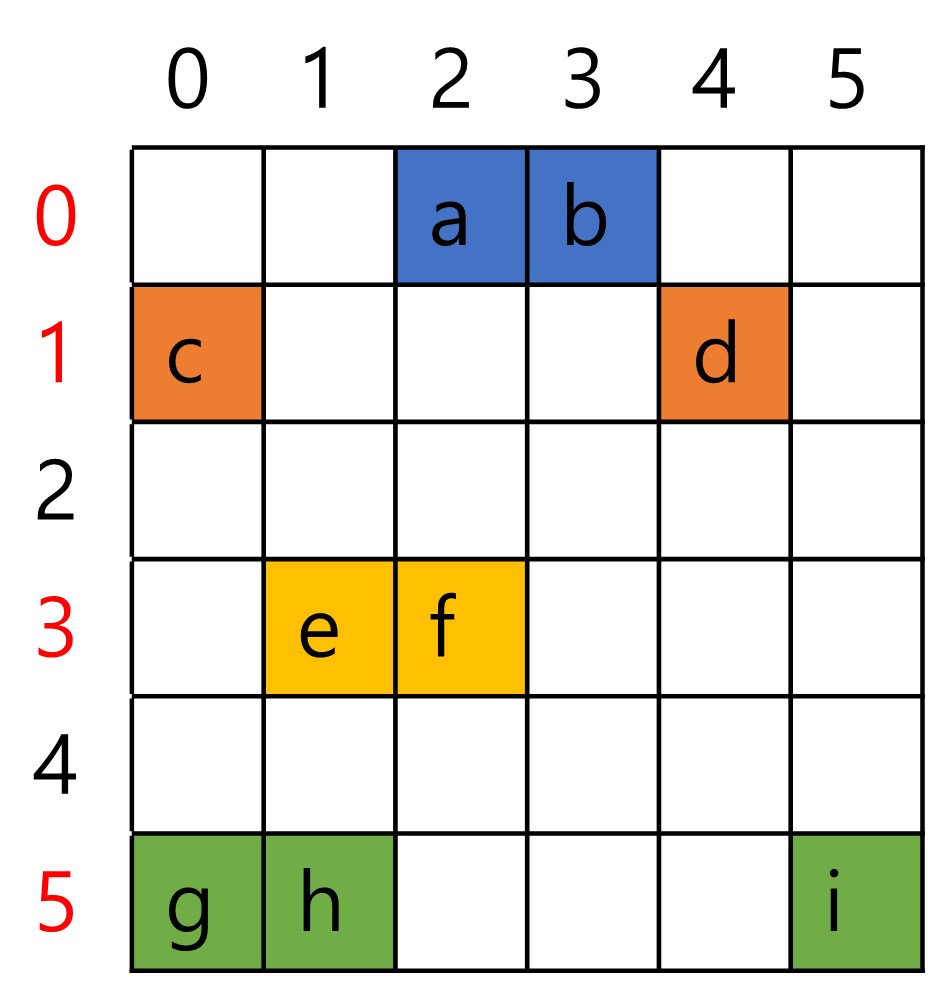
바로 위의 이미지는 행렬의 요소 값이 0인 위치를 빈칸으로 다시 표현한 것이다. 이 희소 행렬의 희소성 (sparsity)은 (0의 수 / 전체 요소의 수) = 27 / 36 = 0.75 정도지만 실제 데이터에서는 희소성이 더 높은 경우가 많기 때문에 압축 포맷을 적용했을 때 데이터의 압축률은 더 높을 수 있다.
아래에서는 위의 희소 행렬이 형태에 따라 각각 어떻게 압축되는지 설명을 진행하고자 한다.
COO Matrix
COO 행렬은 희소 행렬을 표현하는 가장 직관적인 형태로 다른 포맷에 비해 높은 가독성과 데이터 형태의 변환이 쉽다는 장점이 있다. 마치 2차원 좌표계에서 x와 y 값을 표기하듯이 COO 포맷은 희소 행렬의 0이 아닌 요소들의 좌표와 해당 위치의 값을 함께 저장하는 방식이다.

예시 행렬의 각 요소들의 좌표를 (row, column)으로 표기한다면, 값 a의 좌표는 (0, 2)이다. 마찬가지로 나머지 데이터에 대해서 반복 수행을 하면 COO format은 바로 위의 예시 이미지와 같이 표현될 수 있으며 결과적으로 더 적은 수의 메모리를 통해 희소 행렬의 크기를 축소시킬 수 있다.
예시 데이터에서는 원본과 비교하여 압축률이 별로 크지 않아 보이지만 실제 데이터의 경우 희소성이 더 높은 경우가 많기 때문에 메모리를 보다 효율적으로 관리할 수 있다.
CSR Matrix
CSR 행렬은 COO Matrix에서 압축률을 더 높인 형태로 [column, data] 세트에 대해 row 포인터를 붙여준 형태이다. 쉽게 말하면 첫 번째 row가 [column, data] 리스트에서 몇 번째에 해당하는지를 표기하여 row 하나에 값이 2개 이상 있을 경우 불필요하게 row number가 중복되는 것을 방지한 것이다.
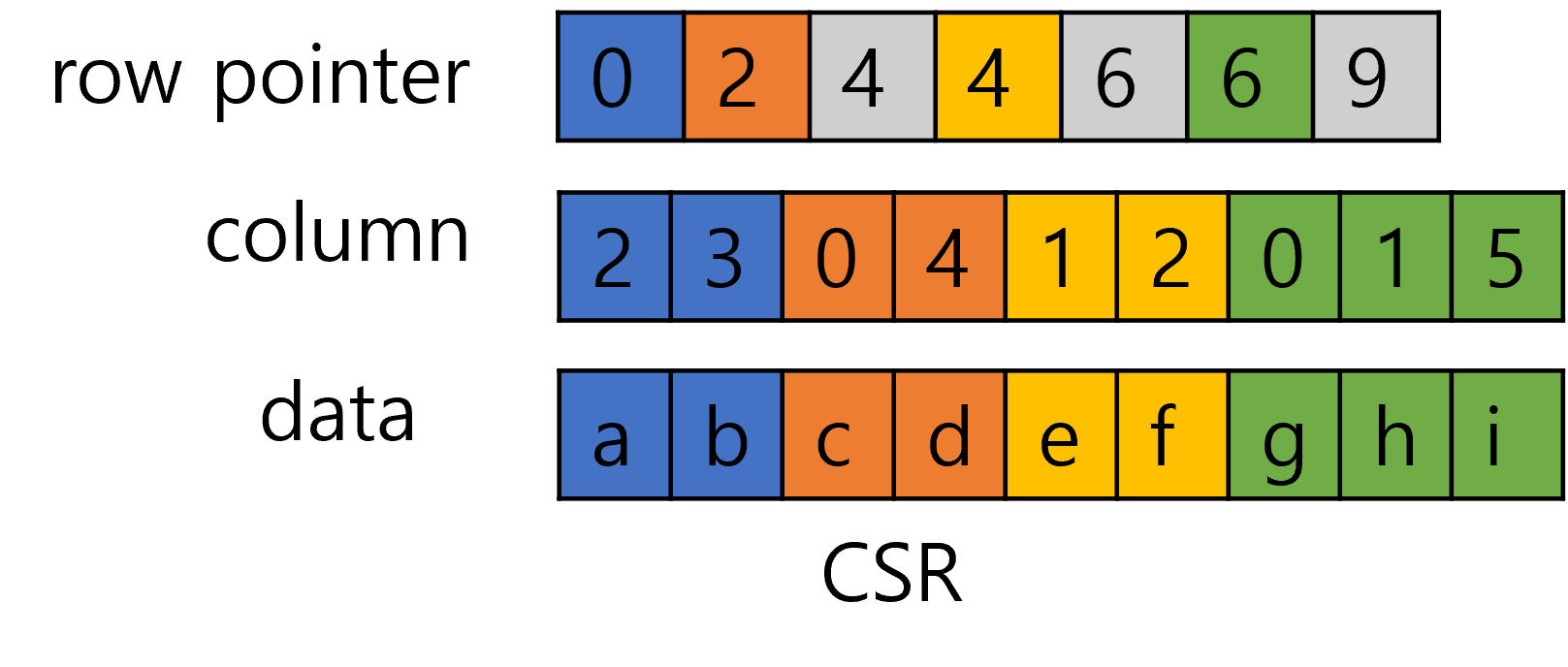
COO Matrix의 경우 하나의 row에 data가 n 개가 있을 경우 n 번 만큼 row index가 반복되어 저장되어야 했다. 만약 row 하나에 data가 100개 존재할 경우 불필요하게 같은 값이 100번 반복되는 것이다. 사실 생각해 보면 [column, data] 리스트에서 0번 row에 해당하는 부분이 어디서부터 시작하고 1번 row에 해당하는 부분이 어디서부터 시작하는지만 안다면 row index를 여러 번 반복해서 사용할 이유가 없다.
CSR Matrix에서는 대신에 row pointer라고 하는 개념을 두어 0번부터 마지막 5번 row까지 어디서 시작하고 어디서 끝나는지를 표기하였다. 위의 row pointer의 규칙은 간단하다. "이상과 미만" 이것만 기억하면 된다.
i번째 row는 row pointer의 i번째 index의 값 이상 (i + 1)번째 index의 값 미만을 의미한다.
따라서 row pointer의 길이는 항상 (row의 수 + 1)개 이며,
여기서는 row의 개수가 총 6개이므로 row pointer의 길이는 (6 + 1) = 7개가 된다.
총 0에서 5번째까지 row pointer를 앞에서부터 한 칸씩 값을 짚어보며 보면,
0번째 row는 [column, data] 리스트에서 0번째 index 이상 2번째 index 미만.
1번째 row는 [column, data] 리스트에서 2번째 index 이상 4번째 index 미만.
2번째 row는 [column, data] 리스트에서 4번째 index 이상 4번째 index 미만.
3번째 row는 [column, data] 리스트에서 4번째 index 이상 6번째 index 미만.
4번째 row는 [column, data] 리스트에서 6번째 index 이상 6번째 index 미만.
5번째 row는 [column, data] 리스트에서 6번째 index 이상 9번째 index 미만.
위의 예시에서는 row pointer가 가리키는 [column, data] 위치를 같은 색으로 나타내고 있다.
2번째 row와 4번째 row의 경우에 이상의 값과 미만의 값이 같으므로 해당 row에 데이터가 존재하지 않음을 의미한다.
따라서 2번째 row와 4번째 row에 해당하는 부분은 row pointer에서 회색으로 나타내었다.
CSR 행렬의 경우 각 row에 0이 아닌 값이 다수 존재할수록 메모리 효율이 커지게 된다.
DCSR Matrix
Dynamic CSR (King, James, et al.) 행렬의 경우 CSR에서의 row pointer 형태를 살짝 더 개선한 형태이다.
CSR 행렬의 경우 2번째와 4번째 row의 값이 모두 0이더라도 row pointer는 해당 영역 (CSR 예시 이미지, row pointer의 회색 영역)을 보존하는 방식을 채택하였지만 DCSR 행렬의 경우, 값이 존재하는 row만 row pointer에 남기고 값이 존재하지 않는 row의 경우 메모리에서 해당 row에 대한 정보를 할당하지 않는다.

위의 이미지에서와 같이 DCSR에서는 CSR의 기본 구조에 row pointer에 대응되는 row index 정보가 추가되었다. 그리고 row pointer에는 더 이상 값이 존재하지 않는 row의 정보를 담고 있지 않는다. row pointer는 더 이상 0번째 row부터 순차적이지 않으므로 반드시 row index를 통해 각 pointer 내 값이 몇 번째 row에 대한 pointer 인지를 확인해야 한다. 덕분에 row pointer는 CSR 행렬과는 다르게 길이가 가변적이다.
DCSR 포맷은 희소 행렬의 많은 row가 0으로 이루어질수록 더 큰 메모리 절감 효과를 얻을 수 있다. 하지만 DCSR 포맷이 실질적으로 CSR matrix에 비해 메모리적인 이점을 보려면 절반 이상의 row가 0으로 이루어져 있어야 한다. DCSR 포맷은 메모리 절감의 효과보다는 (특히 GPU에서의) 연산 상의 이점이나 프로그래밍적 편리성을 위해 사용된다.
DCSR 포맷의 경우 조금 뒤늦게 논문으로 나오기도 하였고 아직 충분한 성능 검증이 되지는 않았는지 scipy에서 공식적으로 지원하고 있지는 않는다.
결론
희소 행렬을 표현하는 위의 세 가지 형태는 각각의 장단점이 존재하기 때문에 상황에 맞게 사용하는 것이 바람직하다. 메모리를 효율적으로 관리하는 것에 유리한 형태가 연산 상의 또는 프로그래밍적 생산성에는 좋지 못할 수 있다.
'데이터 > ML' 카테고리의 다른 글
| Transformer 논문, 쉽게 설명한 사이트 정리 (0) | 2023.11.14 |
|---|

